-
디퓨전 모델(Diffusion Model): 사전지식카테고리 없음 2023. 6. 22. 22:55
디퓨전 확률모델(Diffusion Probabilistic Model), 줄여서 디퓨전 모델(Diffusion Model)을 공부하다 알게된 용어들과 개념들을 정리해본다.
Langevin dynamics
- 랑쥬뱅(Langevin)이라는 프랑스 물리학자가 발명한 이론으로 처음에는브라운 운동(brownian motion)을 설명하기 위해 사용되었다.
Langevin Monte Carlo: Sampling using Langevin Dynamics
A tutorial on how to sample from a distribution using Langevin Dynamics, why it works.
perceptron.blog
재밌는 사실은 랑쥬뱅은 뛰어난 물리학자이자, 그 유명한 퀴리부인과 .... 이었다는 사실
자세한 내용은 아래를 참조.
https://www.dongascience.com/news.php?idx=-5256582
대한민국 1등 과학브랜드, 동아사이언스
모든 사람에게 즐거운 과학을 선물합니다 깊이 있는 전문적인 과학뉴스와 일상생활 속 과학 상식까지 국내 NO.1 과학 포털에서 '즐거운 과학'을 만나보세요!
www.dongascience.com
다만, 랑쥬뱅 dynamics에 대해서는 나중에 깊이 공부해보야아 할 것 같다.
Markov chain
diffusion model 에서 markov 이산확률 과정이 쓰이는데, 단순하게 설명하면
(t+1)의 상태(state)는 바로 이전 상태(t)에만 의존한다는 것이다.

Markov chain Markov 상태를 가정하면
- 계산 복잡도를 줄여준다.
다만, markov 상태가 깨지는 지 항상 확인해보아야 할 것이다.
예를 들면 markov 상태를 적용하면 오늘의 날씨는 어제의 날씨의 상태에만 의존한다고 가정하게 되는데, 실제로는 그렇지 않을 수 있다.
Normalizing Flow
diffusion model 의 아이디어를 얻는데 많은 영향을 미친 것으로 보이는 개념이다.
심층신경망 기반 확률적 생성 모형 중 하나로, 잠재변수(Z) 기반 확률 생성 모형이다.
잠재변수(Z) 획득에 ‘변수변환’ 공식 활용하는 것이다.
예를 들면 어떤 쉬운 분포 (gaussian) z 에, invertable한 연산 f들을 해 주어서, 결국 복잡한 확률분포 px(x)를 모델링 할 수 있도록 하는 것이다.
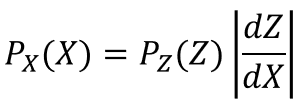
여기서 f = |dZ/dX] 가 될 터인데, 아주 개념화하자면 이런 것이고 실제로는 여러번 반복하거나, 복잡한 chain 형태로 구현될 것이다.
Normalizing Flow와 딥러닝
Normalizing Flow의 정의와 특징을 알아봅니다. 딥러닝으로 Normalizing Flow를 구현하기 위한 조건을 살펴봅니다. 마지막으로 딥러닝으로 Normalizing Flow를 구현한 모델인 NICE, RealNVP, Glow를 살펴봅니다.
ffighting.net
를 참조해보자면 다음의 그림으로 표현 가능하다.

고차원의 데이터를 표현하기 위해서는 매우 복잡한 함수 형태가 필요하므로, 확률 계산이 tractable 하지 않다. 이를 변환 f를 통해 충분히 tratable 한 function으로 변환한 후, 다시 역변환을 취하는 꼴이다.
이를 VAE와 비교해보면 다음의 표로 표현 가능하다.

아래에 여전히 익숙치 않은 용어들... 나중에 천천히 공부해봐야 겠다.
- nonequilibrium thermodynamics
- energy-based modeling
- score matching